More on adoption of electric cars

In my previous post on going electric I looked at the total generating capacity in the United States as compared to average usage and the electrical requirements of replacing the U.S. personal transportation fleet with electric vehicles. Of course, this is the most cursory look possible. Among other things, as Geoffrey Styles of the blog "Energy Outlook" pointed out, efficient management of the grid via utilization of available capacity at times of low baseline consumption would be required and might even be sufficient.



It's also clear that it wouldn't be the case that on, say December 31, 2011 there would be almost no electric cars on the road (as today) and on January 1, 2012 all personal vehicles would be electric. Mathematicians have developed several methods that purport to model the adoption and spread of technology. Among these are the logistic function and the Gompertz function. So what might the adoption and market penetration of electric vehicles look like, and how quickly, if at all, would generating capacity need to be added?



In reply to President Obama's call for one million plug in hybrids and electric vehicles, Nissan CEO Carlos Ghosn has stated that this number could be easily surpassed.



Based on a paper concluding that the logistic function best represented the adoption of cellular phones in Taiwan, I'm going look at the logistic function and adjust the coefficients so that the ultimate adoption is 235,000,000 vehicles and 2,000,000 are on the road in 2015. I'll estimate an annual growth rate of 20%. The resulting logistic equation is N = ((235x10^6) 2000000)/(2000000+233000000 e^(-0.2 t)) where N is the total number of electric vehicles and t is the time in years. Using Wolfram Alpha (if you click this link, the equation will already be input, you can change the parameters at will) the plot looks like this:







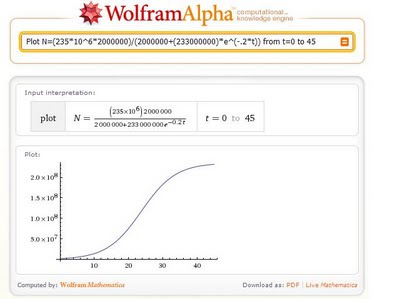
Given that it's said that readership in a blog is reduced by half for every equation posted I'm reluctant to say it but, using calculus, we can determine the rate of change of the population of electric vehicles (that is, how many electric vehicles will be added each year) and determine, at any given time, approximately how much additional demand on the grid will accrue. If we differentiate the equation above (this is kind of backwards in that the logistic equation stems from a differential equation representing the rate of change) we get: d/dt(((235x10^6) 2000000)/(2000000+233000000 e^(-0.2 t))) = (2.1902*^22 e^(-0.2 t))/(233000000 e^(-0.2 t)+2000000)^2. The plot looks like:







At the risk of completely alienating every reader, we can find the maximum rate of addition by taking the second derivative, setting it equal to 0 and solving for t. Plugging this t back into the first derivative and evaluating will give us the maximum rate of addition. But this is such a cascade of estimates that I'll spare the details and just look at the graph. It appears that the maximum rate is about 12,000,000 electric vehicles per year in 2039. That's a long way out and such predictions are obviously fraught with possibilities for error. But I don't know how to do any better.



How much capacity will these 12,000,000 added vehicles per year demand? Let's assume that each vehicle travels 12,000 miles per year and uses 0.2 kilowatt-hours/mile. Further, similarly to the previous post on electric cars linked above, I'm going to assume that the overall efficiency of the transmission and charging systems, we'll need to generate twice what the vehicle uses, or 0.4 kilowatt-hours/mile. So, we'll need to generate 12,000,000 cars*12,000 miles/car/year*0.4 kilowatt-hours/mile=57.6*10^9 kilowatt hours/year. Google's calculator conveniently converts this to 6,570 megawatts or about 6.6 gigawatts of added capacity per year required at the peak. A modern large generating facility will have a nameplate capacity of about a gigawatt so this seems eminently achievable using nuclear power or with the invention of, as my friend Michael likes to say, the boron guy.